- Set Up
- Given a population described by a
random variable Y. Suppose
that the distribution of Y is known except for one or more
population parameters,
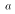 .
.
- Example
- Suppose Y is the number of cigarettes and we know (or assume)
that Y is normally distributed, but we don't know Y's mean
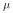 . In this
case, the unknown parameter
. In this
case, the unknown parameter 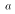 equals
equals 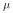 .
.
- We observe N observations from the population, called a sample:
- Sample =
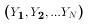
- Each observation in the sample can be thought of as a different
random variable. The actual value in the data set for observation 10
is a realization of the corresponding random variable Y_10.
- We can think of the sample space here as all possible outcomes in a data set:
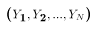 .
.
- Estimation from a Sample
- An Estimator is in general terms simply
- a function of a sample space
- Basic Properties that all Estimator share
- Because an estimator is a function of the sample space, then it is a random variable.
- Because an estimator is a random variable, it has a distribution, a mean, a variance, etc.
- Because estimators have distributions, they have statistical properties
- Because estimators are functions of sample information, they are usually represesnted by formulas or procedures
- Desirable Properties than Estimators May or May not Have.
- Let
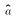 be an estimate of some population parameter
be an estimate of some population parameter
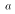 .
.
- Unbiased
![$E[\hat{a}] = a$](../images/glo041.gif)
- In words: Across samples, average value of
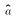 equals
the value of the population parameter
equals
the value of the population parameter 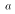 .
.
- Asymptotically Unbiased (with sample size n)":
![$\lim_{n\to\infty} E[\hat a(n)]=a$](../images/glo042.gif)
- In words: With ``enough" data, the estimator is unbiased.
- Asymptotically Normal
![$\lim_{n\to\infty} \hat{a}(n) \sim N(E[\hat{a}(\infty)],Var[\hat{a}(\infty)])$](../images/glo043.gif)
- In words: With "enough" data, the distribution of the estimator becomes the normal distribution.
- Consistent - requires two things of
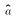 :
:
- 1. Asymptotically Unbiased
- 2. Asymptotically Variance of estimator goes to 0:
![$\lim_{n\to \infty} Var[\hat a(n)] = 0$](../images/glo044.gif)
- In words: With enough data the distribution of the estimator collapses onto the true value.
- Example: Estimation of the population mean
- The usual estimator for the population mean is
the
sample mean (let's call it
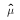 ):
):
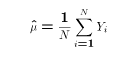
- Notice
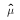 is a function (formula).
is a function (formula).
- Since
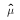 is a function of
random variables, it is a random variable itself. Its value
is not determined until the sample is drawn from the population.
The usual estimator for the population variance
is
is a function of
random variables, it is a random variable itself. Its value
is not determined until the sample is drawn from the population.
The usual estimator for the population variance
is
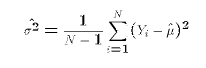
- For a given sample (realization of all the Yi's),
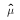 takes on a particular
value. But the sample mean, as a concept, is a function and
a random variable. It is not conceptually a number.
takes on a particular
value. But the sample mean, as a concept, is a function and
a random variable. It is not conceptually a number.
- Statistical Properties of
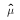 and
and 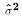
![$E[\hat{\mu}] = \mu$](../images/glo049.gif)
- In words: The mean of the sample mean is the population mean. It is an unbiased estimator.
![$Var[\hat{\mu}] = \sigma^2 / N$](../images/glo050.gif)
- In words: The variance of the sample mean is the variance of the underlying random variable divided by the sample size. It follows directly that
![$\lim_{N\to \infty}Var[\hat{\mu}]=0$](../images/glo051.gif) .
.
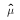 is a consistent estimate of
is a consistent estimate of 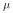 . This
follows directly from the first two properties.
. This
follows directly from the first two properties.
![$E[\hat\sigma^2] = \sigma^2$](../images/glo052.gif)
- In words: the sample variance is an unbiased estimator of
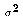 .
.
- The Central Limit Theorem:
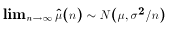
- In words: The distribution of the sample mean for any population converges to a normal distribution as the sample size approaches infinity.
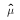 and
and 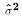 are independently
distributed. This imples that
are independently
distributed. This imples that
![$$E[(\hat{\mu}-\mu)({1\over\hat\sigma^2})] = 0$$](../images/glo054.gif)
- In words: The mean of the sample mean is the population mean. It is an unbiased estimator.
- Note that the variance of
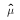 depends
upon the variance of the random variable itself
depends
upon the variance of the random variable itself
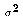 .
.
- The Estimated Variance of the sample mean
![$\hat{Var}[\hat{\mu}] \equiv \hat\sigma^2 / N$](../images/glo055.gif)
- The Estimated Standard Error of the sample mean
![$\hat{se}[\hat{\mu}] \equiv \sqrt{\hat{Var}[\hat{\mu}]}$](../images/glo056.gif)
- You can see the Central Limit Theorm in action by running the tutorial for week 2.
- Since
This document was created using HTX, a (HTML/TeX) interlacing program written by Chris Ferrall.
Document Last revised: 1997/1/5
