Queens University at Kingston

HyperMetricsNotes

glossary File 2
[glossary Contents] [Previous File] [Next File]

B. Random Variables

A Random variable is a real-valued function defined on a sample space

In words:Some measurable aspect of a random experiment.
Types of random variables:
discrete
takes on a finite number of values
Example: number of students who fail a class
continuous
takes on a continuous number of values
Example: high temperature today in Kingston
dummy or categorical
a discrete random variable that indicates non-numerical random outcomes
Example: 0=male student,1=female student
Note: Functions of r.v. are themselves r.v. For example, if Z = ln Y and Y is a random variable, then Z is also a random variable

Cumulative Distribution Function (cdf) for a random variable X

is defined as F(x) = P(X < = x)
probability that X takes on a value < = to x

Some Properties of CDF

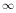  1. F(-$\infty$ ) = 0 (X can't be equal to -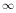$\infty$
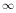  2. F(+$\infty$ ) = 1 (X has to take on some value)
  3. if x > y then F(x) >= F(y) (the cdf is a non-decreasing function in its argument)

Probability or Density function for a r.v. is defined as f(x) = dF(x)/dx [for continuous] and f(x) = P(X=x) [for discrete]

Conditional Probability (cumulative and density)

F(x | A ) = Prob(X<=x | A)
f(x | A ) = dProb( X<=x | A)

Population Parameter is any numerical value or vector of numerical values associated with the distribution of a random variable.

Population Parameters we are often interested in:
mean, variance, median, standard deviation, etc.
[glossary Contents] [Next File] [Top of File]

This document was created using HTX, a (HTML/TeX) interlacing program written by Chris Ferrall.
Document Last revised: 1997/1/5