- Expected Value of a function g(R)
of a random Variable R that
has density function f(r) is defined as
![$$E[R] \equiv \int_{-\infty}^{+\infty} g(r)r f(r) dr$$](../images/glo006.gif)
- Two Common expectations associated with a random variable R
- The Mean (
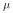) of R is
![$\mu \equiv E[R]$](../images/glo008.gif)
, which is the case g(R) = R.
That is,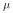
is a synonym for
the expected value of a random variable. When there is more than one random
variable defined, the name of the random variable is a subscript, e.g.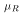 
).
Expectation of the random variable itself.
- The Variance
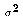of R
is ![$Var[R] \equiv E[ (R-\mu)(R-\mu) ]$](../images/glo011.gif)
.
(
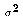is a synonym for the variance of a random variable.)
That is, define the function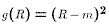 
, then
Var(R) = E[ g(R) ]
The Standard Deviation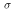 
is the square root of the variance.
If the random variable is an estimator
then its standard deviation is usually called its standard error,
denoted se.
- Properties of Means
Let, a,b, and c be non-random variables (constants)
and let R and S be random variables
- E[a] = a (expected value of a constant is itself)
- E[aR + b] = aE[R] + b (expectation is a linear operator)
- E[aR + bS + c] = aE[R] + bE[S] + c
(E is linear no matter how many random variables are involved)
- If R and S are independent then E[RS] = E[R]E[S]
multiplying two random variables is not a
linear operation ( R*R = R²). So only under
special conditions does the expected value of
the product equal the product of the expected
values. THe special condition being
independence, which is defined below.
- You can see the properties of expectation in action
by running the
tutorial for week 1.
- Properties of Variance
Note that since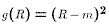
is not a linear function of R,
doing linear things to R does not do linear things
to Var(R).
- Var(a) = 0 (constants don't vary)
- Var(aR+b) = a²Var(R)
(variance affected by square of scaling factor)
- Var(aR + bS ) = a²Var(R) + b²Var(S) + 2abCov(R,S)
(Cov defined below)
- The Mean (
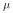) of R is
, which is the case g(R) = R.
That is,
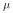is a synonym for
the expected value of a random variable. When there is more than one random
variable defined, the name of the random variable is a subscript, e.g.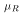
).
Expectation of the random variable itself.
- The Variance
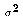of R
is
.
(
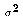is a synonym for the variance of a random variable.)
That is, define the function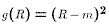
, then
Var(R) = E[ g(R) ]The Standard Deviation
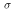is the square root of the variance.
If the random variable is an estimator
then its standard deviation is usually called its standard error,
denoted se.
- Properties of Means
Let, a,b, and c be non-random variables (constants)
and let R and S be random variables
- E[a] = a (expected value of a constant is itself)
- E[aR + b] = aE[R] + b (expectation is a linear operator)
- E[aR + bS + c] = aE[R] + bE[S] + c (E is linear no matter how many random variables are involved)
- If R and S are independent then E[RS] = E[R]E[S]
multiplying two random variables is not a linear operation ( R*R = R²). So only under special conditions does the expected value of the product equal the product of the expected values. THe special condition being independence, which is defined below.
- You can see the properties of expectation in action
by running the
tutorial for week 1.
- Properties of Variance
Note that since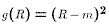
is not a linear function of R,
doing linear things to R does not do linear things
to Var(R).
- Var(a) = 0 (constants don't vary)
- Var(aR+b) = a²Var(R)
(variance affected by square of scaling factor)
- Var(aR + bS ) = a²Var(R) + b²Var(S) + 2abCov(R,S)
(Cov defined below)
- Properties of Variance
Note that since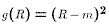
is not a linear function of R,
doing linear things to R does not do linear things
to Var(R).- Var(a) = 0 (constants don't vary)
- Var(aR+b) = a²Var(R) (variance affected by square of scaling factor)
- Var(aR + bS ) = a²Var(R) + b²Var(S) + 2abCov(R,S) (Cov defined below)