Queens University at Kingston

HyperMetricsNotes

glossary File 4
[glossary Contents] [Previous File] [Next File]

D. Joint Distributions

Let X and Y be two random variables defined on the same sample space.

Example:

Sample Space
all undergraduate at Queen's
X
amount of outside study time put in by student (per day)
Y
overall average marks of the student

The Joint Cumulative Distribution of X and Y is defined as F(x,y) = P(X < = x & Y < = y)

Example (continued)
F(24,100) = 1
all students study less than 24 hours a day and all have averages less than or equal to 100
F(0,0) = 0
no students study less than 0 hours and have averages less than or equal to 0.

Joint density of X and Y is defined as f(x,y) = Prob( X= x & Y = y) [discrete] and f(x,y) = d² F(x,y) / dxdy [continuous]

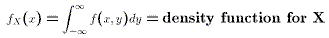
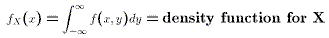
The marginal density function for X is $f_X(x) \equiv \int_{-\infty}^{\infty}f(x,y)dy$

Notice that the marginal density is the same as the ordinary density for the single randome variable. The other random variable Y is integrated out (doesn't matter what value it takes on).

X and Y are (statistically) Independent if and only if
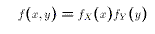
$$f(x,y) = f_X(x) f_Y (y)$$
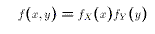
for all values of x and y

In words: if the joint density factors into the product of the two marginal densities then X and Y are said to be independent.

Joint Expectations: Given a joint density function f(x,y) and a function g(x,y) that is a function of the two random variables X and Y, the expected value of g(x,y) is defined as
$$E[g(x,y)] \equiv \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} g(x,y)f(x,y)dxdy$$

Examples of joint expectations:

  1. The mean of one of the random variables can be written using the joint density function:
    $$E[Y] = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} yf(x,y)dxdy = \int_{-\infty}^{+\infty}yf_Y(y)dy.$$
    This is the case where g(x,y) = y.
  2. Covariance is defined as E[ (X-E[X])(Y-E[Y]) ]
    Covariance extends The notion of variance to two dimensions. Its value measures the linear relationship between r.v. Positive covariance indicates that when X is above its mean then Y tends to be above its mean as well - positive statistical relationship. Negative covariance indicates that when X is above its mean Y tends to be below its mean - negative statistical relationship
  3. Correlation between two random variables (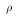$\rho$ ) is defined as
    $$\hbox{corr}(X,Y) \equiv {\hbox{Cov}[X,Y] \over \sqrt{Var[X]Var[Y]} }$$
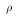    ($\rho$ is a common synonym for corr).

Properties of Covariance

  1. X and Y independent 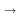$\rightarrow$ Cov[X,Y] = 0
  2. Cov[X,Y]
  3. If X and Y are normal random variables then Cov[X,Y] = 0 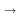$\rightarrow$ X and Y independent.
    Note that Cov[X,2Y] = 2Cov[X,Y], so a simple linear change in the random variables will increase or decrease the size of their covariances. Correlation avoids this scaling effect.

    Properties of Correlation

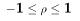
    1. $-1 \le \rho \le 1$
    2. Cov[X,Y] = 0 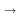$\rightarrow$ corr[X,Y] = 0 (Zero covariance is the same as zero correlation)
    3. If X and Y are linear functions of each other, then |corr[X,Y]| = 1.
    4. corr[aX,bY] = corr[X,Y]
      The absolute value of corr[X,Y] measures the degree of linear relationship between them. The sign of corr[X,Y] indicates whether there is a positive or negative relationship between X and Y. Unlike covariance, correlation is unaffected by the scaling of the random variables by constants.

      Example of Joint Distribution

      Let X take on the values 1, 2
      Let Y take on the values 0,1 
      
                                     f (x)
       f(x,y)    0         1          X
             --------------------
      1     |  0.1    |   0.3    |   0.4
            |_________|__________|
            |         |          |
      2     |  0.4    |   0.2    |   0.6
            ---------------------
     f (y)     0.5        0.5        1.00
      Y
      Confirm the following
      E[X] = 1.5
      E[Y] = 0.4
      Var(X) = 0.25
      Var(Y) = 0.24
      X and Y are not independent
      E[X | Y=0 ] = 1.8

      You can get as much practice as you want with this kind of example by running the tutorial for week 2.

[glossary Contents] [Next File] [Top of File]

This document was created using HTX, a (HTML/TeX) interlacing program written by Chris Ferrall.
Document Last revised: 1997/1/5