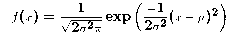
where
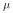 is
the mean of X and
is
the mean of X and 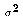 is the
variance of X.
is the
variance of X.We indicate that X is a normal random variable by writing: X ~ N(
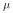 ,
,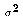 )
)
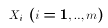 Let Z1, Z2, ... , Zk be k independent standard
normal random variables. Then the function
Let Z1, Z2, ... , Zk be k independent standard
normal random variables. Then the function
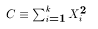
follows the chi-squared distribution with k degrees of freedom. We write
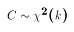 or sometimes
or sometimes 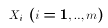 .
.
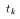 Let Z ~ N(0,1) and C ~
Let Z ~ N(0,1) and C ~ 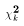 where Z and C
are indendent. Then the function
where Z and C
are indendent. Then the function
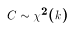 follows the
follows the 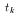 distribution.
distribution.
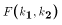 :
Let
:
Let 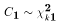 and
and
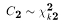 be indpendently distributed.
Then the function
be indpendently distributed.
Then the function
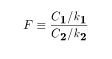
follows the follows the
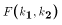 distribution.
distribution.

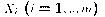 be m
normally distributed random variables, and let
be m
normally distributed random variables, and let 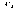 be
m constants. Then the random variable
be
m constants. Then the random variable
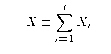
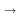 X and Y independent.
X and Y independent.