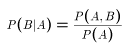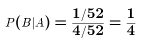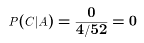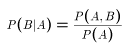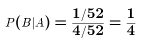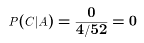The Sample Space is the set of all possible outcomes from a random experiment.

Example

the random experiment of drawing one card from a deck has a sample space with 52 elements (outcomes):

S = { (2,Diamonds), ...., (Ace,Diamonds), (2,Hearts), ...., (Ace,Hearts), (2,Clubs), ..., (Ace,Clubs), (2,Spades), ..., (Ace,Spades) }

Event is a subset of the sample Space

Example

the event of drawing a three is

A = { (3,Diamonds), (3,Hearts), (3,Clubs), (3,Spades) }

An event can be a simple outcome:

B = { (3,Spades) }

C = { (8,Hearts) }

Probability is afunction that maps events into the range [0,1]

Example (continued from above)

in a fair deck

P(A) = 4/52 P(B) = 1/52 P(A & C) = 0 (A and C can't occur simultaneously)

Some laws of Probability

1. P(Ø) = 0
   probability of nothing happening is 0

   P(S) = 1

   The probability of something happening is 1

   P(A U B) = P(A) + P(B) if A and B are mutually exclusive

   probability is additive over distinct events

Events A and B are independent if and only if P(A & B) = P(A)*P(B)

Conditional Probability: P( B | A) = probability that event B occurs given (conditional) that event A has occurred.

Bayes Theorem:

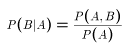
In words: given A has occurred, the probability that B also occurs is the probability that they both occur divided by the probability that A occurs.

Example (using events A, B, and C defined above)

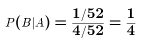
In words: There is a 1/4 chance that a 3 is also a Spade

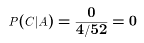
In words: There is no chance that any 3 is also the 8 of Hearts.