- Assumption A2 about the LRM
- The sample information is generated from the PRE.
- That is, the linear relationship between X and Y is the actual relationship between the variables in the data set. This is a critical assumption. If at some point we don't think that we can write down the form of the relationship between X and Y, then it is difficult to say anything about the relationship.
- Assumption A3 about the LRM
- The variable X is non-random across samples.
- That is, our analysis will presume that if another sample were taken from the PRE then: the value
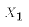 would be the same as before (but
would be the same as before (but
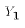 would differ because of a different draw of
would differ because of a different draw of 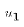 );
the value of
);
the value of 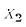 would be the same as before
(but
would be the same as before
(but 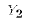 would differ because of a different draw of
would differ because of a different draw of 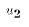 );
etc.
We are not assuming that X is constant within a sample,
but across samples. And we are explicitly assuming
);
etc.
We are not assuming that X is constant within a sample,
but across samples. And we are explicitly assuming - When the sample comes from a real experiment, the values of X are under the control of the researcher. In these cases, A3 is not difficult to maintain. For example, recall the example of sampling young Canadians and asking about their sex (obviously exogenous) and the number of cigarettes they smoke (obviously endogenous). Suppose person 1 in the sample is male (
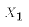 = 0) and person 2 is female (
= 0) and person 2 is female (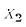 = 1).
If we think about taking a second sample of 600 people, then A3
implies that
= 1).
If we think about taking a second sample of 600 people, then A3
implies that 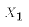 would again equal 0 and
would again equal 0 and 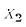 would again equal 1.
We are not assuming that person 1 is the same person
in each sample, but simply the same sex in each sample. Therefore,
the endogenous variable,
would again equal 1.
We are not assuming that person 1 is the same person
in each sample, but simply the same sex in each sample. Therefore,
the endogenous variable, 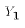 , would differ across samples, but according
to A3 the exogenous variable is assumed to be the same.
, would differ across samples, but according
to A3 the exogenous variable is assumed to be the same.
- With most economic data, another sample of data would most likely involve different values of X. For example, if we re-study the issue of minimum wages five years later and used data from the intervening years, we would most likely have new values of X that didn't appear in the earlier sample.
A3 would then appear to be a difficult to take seriously. But all of our results can be derived from much weaker assumptions. In particular, the actual assumption that we need to make is
- Assumption A3*
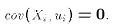
- See covariance. That is, the important part of A3 is not that
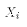 is the same across
samples. If it is the same, then
is the same across
samples. If it is the same, then 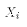 is non-random across samples and a
non-random variable (i.e. constant) always have zero covariance with any
other random variable, in this case the disturbance term
is non-random across samples and a
non-random variable (i.e. constant) always have zero covariance with any
other random variable, in this case the disturbance term 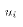 . So A3 implies
A3*, but the reverse is not true. A3* is the
assumption that really matters for our purposes, but it is much simpler
to start with A3 and think of X as non-random.
. So A3 implies
A3*, but the reverse is not true. A3* is the
assumption that really matters for our purposes, but it is much simpler
to start with A3 and think of X as non-random.
- That is, the linear relationship between X and Y is the actual relationship between the variables in the data set. This is a critical assumption. If at some point we don't think that we can write down the form of the relationship between X and Y, then it is difficult to say anything about the relationship.
- Assumption A4
![$E[ u_i ] = 0$](../images/reg131.gif) for
for 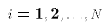
- The disturbance term has mean of 0.
- Assumption A5
![$Cov[u_i,u_j] = 0$](../images/reg133.gif) for
for 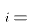
- (The disturbance terms in any two observations have no covariance, and hence are uncorrelated.)
- Assumption A6
![$Var[u_i] = \sigma^2$](../images/reg135.gif) for
for 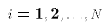
- Each disturbance term has the same variance, an unknown population parameter
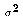 .)
.)
- Assumption A7
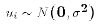 for
for 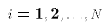
- (That is, the disturbance follows the normal distribution for each observation in the sample.)
- The disturbance term has mean of 0.
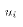 's to ensure that OLS estimates are "good". A4
is really a "technical" assumption. It says that on average the disturbance
terms are 0. We already have an intercept term
's to ensure that OLS estimates are "good". A4
is really a "technical" assumption. It says that on average the disturbance
terms are 0. We already have an intercept term  that is freely
estimated. The disturbance term u is therefore a deviation from
that is freely
estimated. The disturbance term u is therefore a deviation from  and u can have a mean of 0 without imposing any restriction on the model.
A4 is called a normalization, because if we dropped A4 we could
change some other assumption (set
and u can have a mean of 0 without imposing any restriction on the model.
A4 is called a normalization, because if we dropped A4 we could
change some other assumption (set  = 0) and get back to
the same model.
= 0) and get back to
the same model.A5 and A6 are more important than A4. A5 says that the different observations in the data set do not have statistically related disturbance terms. Notice, we didn't say "independent," because independence is a stronger assumption than 0 covariance. In fact, independence between two random variables is very hard to test, but checking or testing whether the disturbance terms have 0 covariance is not difficult.
A6 says that each of the disturbance terms has the same variance, 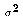 .
It assumes that each observation has equal variance around the PRE. This
means each observation provides the same information (in a sense made clear
later) about where the PRE is located. If, instead, some
observations had lower variances than others,
then the low variance observations tend to be closer to the PRE. When
trying to find the PRE (by estimating
.
It assumes that each observation has equal variance around the PRE. This
means each observation provides the same information (in a sense made clear
later) about where the PRE is located. If, instead, some
observations had lower variances than others,
then the low variance observations tend to be closer to the PRE. When
trying to find the PRE (by estimating  and
and  )
we would want to put more weight on the low variance observations.
The term ordinary least squares really
means equally weighted least squares, and Assumption A6
about the distribution of
)
we would want to put more weight on the low variance observations.
The term ordinary least squares really
means equally weighted least squares, and Assumption A6
about the distribution of 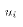 therefore relates to the performance of OLS.
therefore relates to the performance of OLS.
 Until introduced to the LRM, people are usually not comfortable with
a statistical relationship like the PRE. Before we go
any further, let us consider the non-statistical
relationship underneath the PRE.
The way that randomness is removed is to integrate out variations
across the sample space. In other words, we eliminate randomness
by taking expectations.
Until introduced to the LRM, people are usually not comfortable with
a statistical relationship like the PRE. Before we go
any further, let us consider the non-statistical
relationship underneath the PRE.
The way that randomness is removed is to integrate out variations
across the sample space. In other words, we eliminate randomness
by taking expectations.
![$$\eqalignno{E[Y_i|X_i] &= E[ \beta_1 + \beta_2 X_i + u_i]\cr &= \beta_1 + \beta_2 X_i + E[u_i]\cr\cr E[Y_i|X_i] &= \beta_1 + \beta_2 X \hskip 0.25in (using A2) &(E7)\cr}$$](../images/reg298.gif)
Notice that we are taking the conditional
expectation of 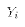 , conditional upon knowing the value of
, conditional upon knowing the value of 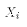 .
Equation E7 is another way to think of the LRM. It says that we
are assuming a linear relationship between the exogenous
variable
.
Equation E7 is another way to think of the LRM. It says that we
are assuming a linear relationship between the exogenous
variable 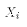 and the expected value
of the random
variable
and the expected value
of the random
variable 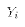 . This is an ordinary linear relationship;
there are no random variables left in E7 because
. This is an ordinary linear relationship;
there are no random variables left in E7 because ![$E[Y_i]$](../images/reg139.gif) is a population
parameter. Taking expectations wipes out the influence of the random
factor
is a population
parameter. Taking expectations wipes out the influence of the random
factor 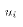 .
.
It is then perfectly legal and reasonable to take derivatives in E7:
![$${\partial E[Y_i|X_i] \over \partial X_i} = \beta_2$$](../images/reg140.gif)
We interpret the slope coefficient  as a derivative, the rate of change in
as a derivative, the rate of change in ![$E[Y_i]$](../images/reg139.gif) as the exogenous variable X
changes. In our minimum wage example,
as the exogenous variable X
changes. In our minimum wage example,  would determine the rate
at which expected employment (across provinces) changes as the minimum wage changes.
Notice that the disturbance term u has no effect on this interpretation. In
others, the level of
would determine the rate
at which expected employment (across provinces) changes as the minimum wage changes.
Notice that the disturbance term u has no effect on this interpretation. In
others, the level of 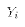 is moved around by the disturbance terms, but
is moved around by the disturbance terms, but
 measures how
measures how 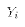 would change with
would change with 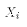 .
.
This document was created using HTX, a (HTML/TeX) interlacing program written by Chris Ferrall.
Document Last revised: 1997/1/5
