- [random variables] [distribution] [expectation]
[conditional expectation]
Sample space = { (0,M), (1,M), (2,M), ......, (50,M) (0,F), (1,F), (2,F), ......, (50,F) }- We could pose our questions about probabilities related
to this sample space, but there are over 100 probabilities
to consider.
- Since sample space is a set notion, it is very general. But numbers of cigarettes smoked and male/female are very specific, organized concepts.
- Approach the data using the concept of a
random variable
- How many random variables do we want to define over this sample space?
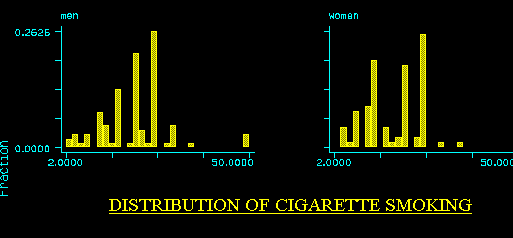
- Y = number of cigarettes smoked ( continuous r.v.)
- X = 0 if male, 1 if female (dummy r.v.)
- Use the notion of expectation to summarize the joint distribution of X and Y.
- Does P(Y=0 | X=male) differ from P(Y=0 | X=female)?
- Does E( Y | X=male) differ from E(Y| X=female)?
- Does E( Y | Y > 0,X=female) differ E(Y | Y>0, X=male)?
- The expressions in the cigarette questions are
population parameters.
How does one estimate
their values when only a sample from the population
is available?
- An estimator is a random variable, but it is not defined on the same sample space as the observations. For instance, in the cigarette example, Y is a random variable defined on the set of all young Canadians. You tell me which young person was contacted (that's the outcome of the random experiment), and I can find out how many cigarettes he/she claims to smoke each day (that's the mapping from outcomes to real numbers). I can also determine whether it is a he or she (that's the mapping for another random variable defined on the same sample space, namely X). However, for me to know what value the sample mean (that's a random variable too) takes on, it is not enough to tell me the name of one young person. If the sample size is N=3, then you need to tell me the names of 3 young people (that's a subset of S, which is not itself a member of S). So the sample mean is defined on events in S.
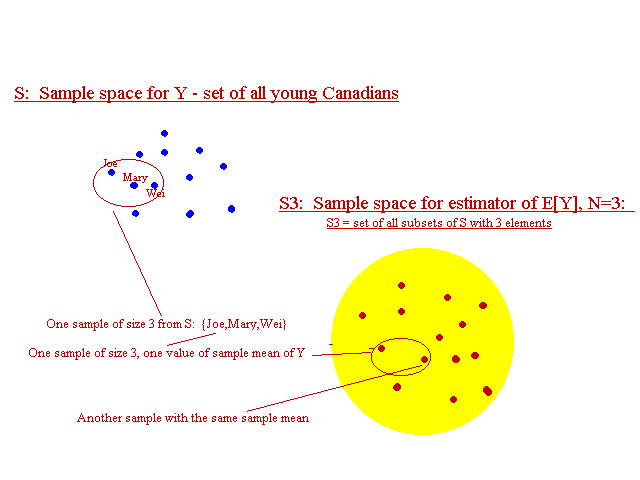 The Sample Space for an Estimator
The Sample Space for an Estimator- We can calculate estimates from the data :
The tables reveal:* log file from a Stata session analyzing the cigs.raw data . use cigs . gen byte any = cond(cigs>0,1,0) . label define sex 1 "men" 2 "women" . label values dvsex sex . tab dvsex, summ(cigs) | Summary of cigs Sex| Mean Std. Dev. Freq. ------------+------------------------------------ men | 6.5333 10.6017 300 women | 4.8933 8.5900 300 ------------+------------------------------------ Total | 5.7133 9.6753 600 . tab dvsex any, row | any Sex| 0 1 | Total -----------+----------------------+---------- men | 201 99 | 300 | 67.00 33.00 | 100.00 -----------+----------------------+---------- women | 214 86 | 300 | 71.33 28.67 | 100.00 -----------+----------------------+---------- Total| 415 185 | 600 | 69.17 30.83 | 100.00 . sort dvsex . by dvsex: summ cigs if any==1 -> dvsex= men Variable | Obs Mean Std. Dev. Min Max ---------+----------------------------------------------------- cigs | 99 19.7980 8.8109 2.0000 50.0000 -> dvsex=women Variable | Obs Mean Std. Dev. Min Max ---------+----------------------------------------------------- cigs | 86 17.0698 7.0190 4.0000 35.0000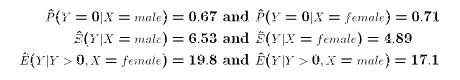
- In words:
- An estimator is a random variable, but it is not defined on the same sample space as the observations. For instance, in the cigarette example, Y is a random variable defined on the set of all young Canadians. You tell me which young person was contacted (that's the outcome of the random experiment), and I can find out how many cigarettes he/she claims to smoke each day (that's the mapping from outcomes to real numbers). I can also determine whether it is a he or she (that's the mapping for another random variable defined on the same sample space, namely X). However, for me to know what value the sample mean (that's a random variable too) takes on, it is not enough to tell me the name of one young person. If the sample size is N=3, then you need to tell me the names of 3 young people (that's a subset of S, which is not itself a member of S). So the sample mean is defined on events in S.
- An estimated 67 percent of young Cdn men don't smoke
- An estimated 71 percent of young Cdn women don't smoke
- Young Cdn men smoke an estimated average 6.53 cigarettes a day
- Young Cdn women smoke an estimated average 4.89 cigarettes a day
- Young Cdn men smoke who smoke at all smoke an estimated 19.8 cigarettes a day
- Young Cdn women smoke who smoke at all smoke an estimated 17.1 cigarettes a day
- An estimated 71 percent of young Cdn women don't smoke
