The poll is based on a sample of 1000 Canadians and is considered accurate to plus or minus 3.1 percentage points.

Question

1. Where does this number 3.1 come from?
2. What does it mean?
3. Why is it the same for all polls of size 1000?

Answer: Preliminaries

Opinion polls are usually based on yes/no questions. For example,

Q: Do you think Jerry Garcia was a good role model?

Define a random variable:

Z = 0 if person says "no, Jerry Garcia was not a good role model"

Z = 1 if person says "yes, ..."

The distribution of Z is determined completely by the the proportion of people for whom Z=1.

Define

P(Z=1) = p

Note:

E[Z] = 0*P(Z=0) + 1*P(Z=1) = 0+p = p

So p is the mean of the random variable Z .

Var[Z] = (0-p)² * P(Z=0) + (1-p)²*P(Z=1)=p²(1-p)+(1-p)² p = p(1-p)

The proportion of people in the survey that say "yes" is an estimate of p:

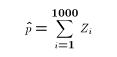
We know in a sample of 1000 that

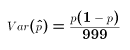
This variance is an unknown population parameter since it depends upon p, and p is an unknown population parameter. At best we can only estimate the variance of p^. A reasonable estimate is

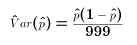
We define the standard deviation of p hat as its standard error. The estimated standard error is therefore

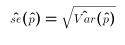
We know from the Central Limit Theorem and the defintion of the t distribution that for large samples,

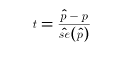
follows the 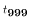distribution.

Answer: Where does 3.1 come from?

"19 out of 20" = 19/20 = 0.95

It follows that

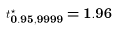
3.1 percentage points equals 0.031

So 0.031 must be the radius of the 95 percent confidence interval for the population parameter p. The newspaper seems to be saying:

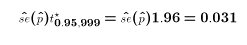
BUt clearly the estimated standard error of p hat depends upon the value of p hat (from the defintion above). Why doesn't it differ from poll to poll based on the number of yeses and nos?

If newspapers don't want to overstate the acccuracy of the results, then they might be reporting the confidence interval for the worst case (half say yes, half say no). If so,

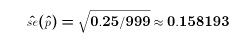
and 0.158193 * 1.96 = 0.03100583

or almost exactly 3.1 percentage points

Answer to: What does 3.1 mean?

Discussion

Example from the cigarette data

* "ci" computes confidence interval for the MEAN of a variable

. ci cigs, by(dvsex) level(90)

->  dvsex=men   
Variable |     Obs         Mean    Std. Err.       [90 Conf. Interval]
---------+-------------------------------------------------------------
    cigs |     300       6.5333      0.6121          5.5234      7.5433

->  dvsex=women   
Variable |     Obs         Mean    Std. Err.       [90 Conf. Interval]
---------+-------------------------------------------------------------
    cigs |     300       4.8933      0.4959          4.0750      5.7116


*    Notice that the standard error (or standard deviation) of 
*    the sample mean is not the same as the std. dev. of the variable
*    itself (i.e. 0.6121 not equal to 10.6017).  We saw in class that 
*    the st.dev. of the sample mean of X is sqrt(Var(X)/N), where N is the
*    sample size.  

*    Does Stata use the same formula that we do to calculate confidence
*    intervals?  Use display (or "di" for short) to find out:

. di 6.5333+invt(299,.90)*0.6121
7.543244

*    Notice 7.543244 is (to 3 digits) the upper bound of the 90 percent interval
*    reported by ci.
*    Also notice the use of the invt function to look up values of the 
*     t distribution.  Get help with invt in the tutorial for week 2

End of Document stats