- [
conditional probability]
- A contestant was shown 3 doors. Behind one door was a nice prize.
Behind the other doors were bad prizes. Let V
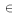 {1,2,3}
denote the
number of the door behind which the prize lies.
{1,2,3}
denote the
number of the door behind which the prize lies.
- The contestant picks a door, call it C,
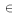 {1,2,3}.
{1,2,3}.
- The show's M.C., Monte Hall, would reveal a door M which was
never door C nor door V. Therefore, behind door M
was always a bad prize: M
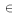 {1,2,3} - {C,V}.
{1,2,3} - {C,V}.
- After the last step, the contestant was asked if they wanted to keep their door (C) or switch to the other unrevealed door U = {1,2,3}-{M,C}. Let F be the door the contestant eventually chooses: F
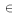 {U,C}.
{U,C}.
- Door F is opened and the contestant gets the prize behind it.
- After the last step, the contestant was asked if they wanted to keep their door (C) or switch to the other unrevealed door U = {1,2,3}-{M,C}. Let F be the door the contestant eventually chooses: F
The sample space is determined by knowing the value of (V, C, M). The possible events can be ordered by whether V=C or not, and by the values of V, C, M.Let's assume that V and C are chosen at random (each door has equal probability). Then the contestant has a 1/3 chance of picking C=V. Furthermore, if C=V then the organizers have a choice of two values to set M to. (For example, if C=V=1 then M can be either 2 or 3.). So the corresponding probabilities for each outcome look like this:C=1 C=2 C=3 S = { (1,2,3), (1,3,2), V=1 not equal C (2,1,3), , (2,3,1), V=2 not equal C (3,1,2),(3,2,1), V=3 not equal C (1,1,2), (2,2,1), (3,3,1), V=C,M=1st possible value (1,1,3), (2,2,3), (3,3,2), V=C,M=2nd possible value }You are half as likely to have picked the right outcome at the start, which you can see by adding up the six 1/18s and getting the probability of V=C to be 1/3. At the time that the contestant must decide whether to switch or not, the value of C and M are known to him/her. Let's make things a lot simpler by setting C=1 and M=2.P = 1/9 1/9 V not equal C events 1/9 1/9 1/9 1/9 1/18 1/18 1/18 V = C events 1/18 1/18 1/18Applying the formula for conditional probability
P(V=1 | C=1,M=2) = P( (V=1) & (C=1) & (M=2) ) / P(C=1,M=2) The denominator is 1/9+1/18 = 3/18 = 1/6. (I got this by finding all cases where C=1 and M=2 in S and then adding their probabilities.) The numerator is 1/18, so
P(V=1 | C=1,M=2) = 1/18 / 1/6 = 1/3. Compare this to
P(V=3 | C=1,M=2) = P( (V=3) & (C=1) & (M=2) ) / P(C=1,M=2) The denominator is still 1/18 (same conditioning event), but the numerator is only 1/9. So
P(V=3 | C=1,M=2) = 1/9 / 1/6 = 2/3.The intuition is the following: You were twice as likely to have guessed wrong on the first round than to have guessed right. The two other doors had equal probability of being V. By revealing M, the game has eliminated one of the doors and the remaining door (U) now has all the probability of having been the right one in the first place. Therefore, in the second choice U is twice as likely to be the right door as C. The contestant should ALWAYS switch doors if he/she wants to maximize the conditional probability of F=V.. (Thanks to - Mike(?) Campbell for coming up with the intuitive answer.)
