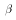 . A
linear restriction on
. A
linear restriction on 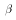 takes the form
takes the form
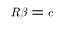
where R is a rxk matrix of constants and c is a r x 1 vector of constants. For example, if k = 5 then the joint hypothesis above could be written:
![$$\left[\matrix{0&1&0&0&0\cr 0&0&1&0&0 \cr 0&0&0&1&0\cr}\right] \left[\matrix{\beta_1\cr\beta_2\cr\beta_3\cr\beta_4\cr\beta_5\cr}\right] = \left[\matrix{0\cr 0\cr 0\cr}\right]$$](../images/mul255.gif)

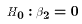 places on restriction
on the possible values of the population parameters. But often we would
like to test multiple hypotheses together. For example,
places on restriction
on the possible values of the population parameters. But often we would
like to test multiple hypotheses together. For example,
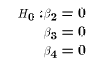
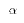 , the probability
of the Type I error, must be controlled for. That means
we must be able to determine the probability of rejecting
, the probability
of the Type I error, must be controlled for. That means
we must be able to determine the probability of rejecting 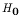 when it
is true. But each of the single t tests ignores the other restrictions,
so setting
when it
is true. But each of the single t tests ignores the other restrictions,
so setting 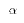 for each test separately doesn't determine the
for each test separately doesn't determine the
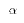 for some combination of them. Without control over
for some combination of them. Without control over 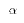 it is
not possible to determine how strongly the data support or don't support
the multiple hypothesis.
it is
not possible to determine how strongly the data support or don't support
the multiple hypothesis.
We therefore need a single test statistic for a multiple hypothesis.
We will restrict attention to linear hypotheses, which are linear
restrictions on the values contained in the parameter vector 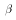 . A
linear restriction on
. A
linear restriction on 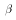 takes the form
takes the form
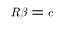
where R is a rxk matrix of constants and c is a r x 1 vector of
constants. For example, if k = 5 then the joint hypothesis above could
be written:
![$$\left[\matrix{0&1&0&0&0\cr 0&0&1&0&0 \cr 0&0&0&1&0\cr}\right] \left[\matrix{\beta_1\cr\beta_2\cr\beta_3\cr\beta_4\cr\beta_5\cr}\right] = \left[\matrix{0\cr 0\cr 0\cr}\right]$$](../images/mul255.gif)
 ). Denote
this
). Denote
this  .
.
 on the OLS estimates, run the resulting regression, and
compute RSS. Denote this
on the OLS estimates, run the resulting regression, and
compute RSS. Denote this 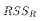 . That is when minimizing the
sum of squared residuals (e'e), we will force the estimates
. That is when minimizing the
sum of squared residuals (e'e), we will force the estimates 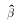 to satisfy
to satisfy 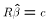 .
Adding a the restriction to the estimates reduces their ability to choose
values for
.
Adding a the restriction to the estimates reduces their ability to choose
values for 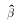 to fit the data. It must be the case that
to fit the data. It must be the case that 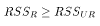 .
.
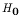 is true
is true
In this world the true parameters actually satisfy the
restriction being imposed on the estimated parameters in the restricted model.
Imposing a true restriction should not make very much difference in the
results.
That is, imposing a true restriction should not change the amount of variation
in Y attributed to the residual u. 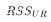 would not
be very different from
would not
be very different from 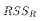 if
if 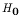 is true. The only reason why
they would differ at all if
is true. The only reason why
they would differ at all if 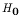 is true is because allowing
is true is because allowing
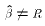 allows the estimates to pick up sampling variation in
the relationship between X and Y. On the other hand,
allows the estimates to pick up sampling variation in
the relationship between X and Y. On the other hand,
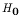 is false,
is false, 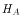 is true
is true
Imposing a false restriction on the estimated parameters
should affect OLS abilitly to fit the Y observations.
That is, if 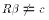 then this should be
would be reflected in
then this should be
would be reflected in 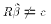 and the RSS in the restricted
and unrestricted models would be much different.
and the RSS in the restricted
and unrestricted models would be much different.
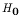 . The ratio (
. The ratio (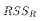 -
-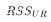 )/
)/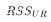 tells us the
proportionate change in the amount of variation attributed to variance in
u when the restriction is imposed. In fact, under
tells us the
proportionate change in the amount of variation attributed to variance in
u when the restriction is imposed. In fact, under 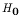 ,
the difference
,
the difference 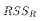 -
-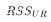 , which is a random variable, is
distributed as a chi-squared
random variable with r degrees of freedom
(the number of linear restrictions), and it is distributed
independently of the unrestricted RSS when
, which is a random variable, is
distributed as a chi-squared
random variable with r degrees of freedom
(the number of linear restrictions), and it is distributed
independently of the unrestricted RSS when 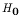 is true. The
intuition for this result is simply that the change in the RSS is due to
explaining the sampling variation if the restriction is indeed true. And
the sampling variation is independent of the model (by assumption u is
drawn independently of everything else going on in the LRM).
is true. The
intuition for this result is simply that the change in the RSS is due to
explaining the sampling variation if the restriction is indeed true. And
the sampling variation is independent of the model (by assumption u is
drawn independently of everything else going on in the LRM).
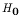 , the expected value of the ratio
is the ratio of expected values.
The mean of a chi-squared random
variable
equals its degrees of freedom. Therefore, the ratio given above would have
a mean equal to r/(N-k) under
, the expected value of the ratio
is the ratio of expected values.
The mean of a chi-squared random
variable
equals its degrees of freedom. Therefore, the ratio given above would have
a mean equal to r/(N-k) under 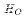 . It makes
sense to normalize the ratio so that is has a mean of 1 under
. It makes
sense to normalize the ratio so that is has a mean of 1 under 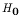 , which
leads to test statistics for linear hypotheses
, which
leads to test statistics for linear hypotheses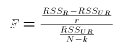
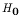 , F follows the F(r,N-k) distribution.
Therefore, we should reject
, F follows the F(r,N-k) distribution.
Therefore, we should reject 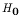 if
if 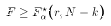 . The
alternative is simply that the restriction is not true:
. The
alternative is simply that the restriction is not true:
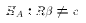
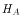 has a greater-than sign and which equations have
a less-than sign.
has a greater-than sign and which equations have
a less-than sign.
When the restriction matrix R contains one row (r=1), then the test
statistic is F(1,N-k). A chi-square random variable
with one degree of freedom is simply a standard normal Z variable squared.
So F(1,N-k) can be written 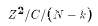 , where C is a chi-squared
with N-k degrees of freedom. But this expression is exactly the
square of a t variable with
N-k degrees of freedom. Hence a t-test is a special case of the
more general F-test.
, where C is a chi-squared
with N-k degrees of freedom. But this expression is exactly the
square of a t variable with
N-k degrees of freedom. Hence a t-test is a special case of the
more general F-test.
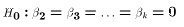 This particular hypothesis (with r=k-1 restrictions)
is called the Consider the hypothesis test for overall
significance. How would you interpret this hypothesis?
Under this
This particular hypothesis (with r=k-1 restrictions)
is called the Consider the hypothesis test for overall
significance. How would you interpret this hypothesis?
Under this 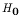 , the linear
regression model would reduce to
, the linear
regression model would reduce to 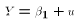 . No X variables
show up in the PRE. So this hypothesis is the hypothesis that
none of the X variables are statistically related to Y. The
alternative is that at least one of the X variables is related to
Y, although which ones that might be is not specified.
. No X variables
show up in the PRE. So this hypothesis is the hypothesis that
none of the X variables are statistically related to Y. The
alternative is that at least one of the X variables is related to
Y, although which ones that might be is not specified.
Notice that the restricted model simply includes a constant. The OLS
estimate of  would in the restricted model be simply
would in the restricted model be simply
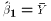 . The
. The 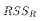 would then simply be TSS! The
restricted unexplained variation is simply the total variation in Y
around its sample mean. Recall that TSS = ESS + RSS, so
would then simply be TSS! The
restricted unexplained variation is simply the total variation in Y
around its sample mean. Recall that TSS = ESS + RSS, so
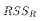 -
- 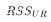 equals TSS -
equals TSS - 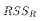 , which equals
, which equals 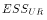 .
So the test statistic for a test of overall significance reduces to
.
So the test statistic for a test of overall significance reduces to
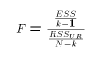
which is simply the ratio of the two MS (mean-squared) entries in the
analysis of variance table. The F statistic reported in
the Stata output table is exactly this number.
We can go even further here. If we have a simple LRM (k=2), then the
test for overall significance collapses to 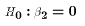 , which we
know can also be tested with the t test
, which we
know can also be tested with the t test 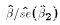 .
But the F version of the test is F(1,N-k), which we know from example
1 is the square of a t test. And, indeed, the overall F statistic is
exactly equal to the the square of the t statistic for
.
But the F version of the test is F(1,N-k), which we know from example
1 is the square of a t test. And, indeed, the overall F statistic is
exactly equal to the the square of the t statistic for 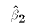 in a simple LRM. You should confirm this fact.
in a simple LRM. You should confirm this fact.
. * Let's test whether expected age of first intercourse
. * differs significantly by religious background
. test none cath oth
( 1) none = 0.0
( 2) cath = 0.0
( 3) oth = 0.0
F( 3, 5590) = 31.10
Prob > F = 0.0000
. * Conclusion: We can reject the hypothesis that
. * expected age of first intercourse is the same for
. * all religious backgrounds
. *
. * Let's perform the F test directly rather than using "test"
. * The regress above is the Unrestricted Model
. qui regress
. di "Unrestricted RSS = " _result(4)
Unrestricted RSS = 27598.636
. local u = _result(4)
. * The Restricted Model imposes H0 on the estimates, which
. * in this case means none cath oth all have zero coefficients
. * So the Unrestricted model is
. regress age
Source | SS df MS Number of obs = 5594
---------+------------------------------ F( 0, 5593) = .
Model | 0.00 0 . Prob > F = .
Residual | 28059.2594 5593 5.0168531 R-squared = 0.0000
---------+------------------------------ Adj R-squared = 0.0000
Total | 28059.2594 5593 5.0168531 Root MSE = 2.2398
------------------------------------------------------------------------------
age | Coef. Std. Err. t P>|t| [95 Conf. Interval]
---------+--------------------------------------------------------------------
_cons | 17.42063 .0299471 581.714 0.000 17.36192 17.47934
------------------------------------------------------------------------------
. di "The Restricted RSS = " _result(4)
The Restricted RSS = 28059.259
. local r = _result(4)
. di "So the F statistic for the test is " ((`r'-`u')/3)/(`u'/(5594-4))
So the F statistic for the test is 31.099197
. * Notice that this is the F statistic reported by test, and
. * since this is a test of overall significance it is also
. * equal to the F statistic reported in the regression output