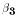related variables.
![$$\eqalign{\hbox{Sample} \equiv [ &(X_{21},X_{31},\dots,X_{k1},Y_1),\cr &(X_{22},X_{32},\dots,X_{k2},Y_2),\cr &\vdots\cr &(X_{2N},X_{3N},\dots,X_{kN},Y_N), ].\cr }$$](../images/mul208.gif)
where
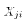is the value of the 
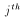variable for the 
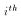observation.
For example, 
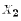might be income, 
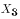might be the price of milk, 
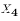might be number of children, etc. Then 
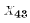equals the number of children in
household (or observation) 3. We begin numbering the X variables at 2 to hold a
place for the constant term.
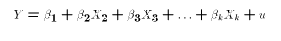
Each coefficient
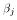is an unknown population parameter. Notice that the
simple linear regression model is the special case of the multiple regression model,
k=2. Since an economic variable like Y is undoubtedly influenced by many
potentially observable influences (like price, income) there is perhaps a better way
to interpret any linear regression model as a special case of a larger (greater k)
model. In particular, we should think of the smaller model as a difference in the
observed sample information. If we do not observe all the factors that influence
Y, then we have a a sample restricted in the X variables that we can observe. We
do not necessarily have the wrong model if we only include one variable in
the regression when there should be many.
The sample for a multiple regression model is written:
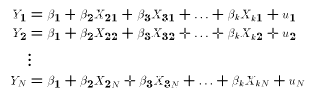
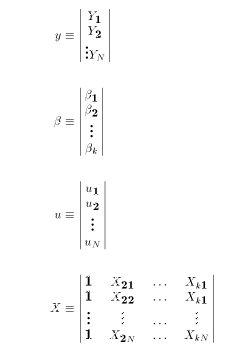
Notice that the subscripts for the matrix X are the reverse of the usual row/column ordering. The reason is that we want to "bind" the variable name first (
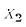refers
to variable number 2), but we naturally write an equation on one line (or row),
forcing us to have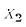
refer to a column rather than a row. With the notation
above, all the sample information is represented by one matrix equation.
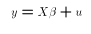
Interpretation of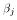
in the LRM
Looking at the PRE equation (**), we can take expectations of both sides:
![$$E[Y_i|X_2,X_3,\dots,X_k] = \beta_1 + \beta_2 X_2 + \beta_3 X_3 + \dots +\beta_k X_k + E[u|X_2,X_3,\dots,X_k]$$](../images/mul221.gif)
Then, using basic calculus we see
![$${\partial E[Y_i|X_2,X_3,\dots,X_k] \over \partial X_j} = \beta_j$$](../images/mul222.gif)
We can interpret the coefficient on the jth variable to be the partial derivative of the expected value of Y with respect to a change in the jth variable. For example, if
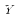is log-consumption of milk and
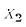is the log of household income, then 
is the income elasticity
of milk demand.
This document was created using HTX, a (HTML/TeX) interlacing program written by Chris Ferrall.
Document Last revised: 1997/1/5