So far we have studied the Simple Linear Regression Model. "Simple"
refers to the fact that only one variable X is related to the endogenous
variable Y. Yet we do not have to look too far to find models in
economics where more than one variable is determining the value of a
variable.
To motivate multiple regression, let's consider the demand for milk by households.
To eliminate the supply curve we will assume that milk is produced with a
constant Marginal Cost technology so that quantities do not affect
equilibrium prices.
Let m be the quantity of milk purchased (say each week) and let 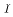 be
household
income. Suppose the household has the utility function
be
household
income. Suppose the household has the utility function
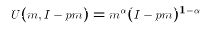
where p is the price of milk faced by the household and U is the
utility function for the household defined in terms of milk and all other
goods. The Marshallian demand function in terms of log milk consumption
takes the form:
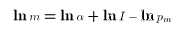
In other words, if the Cobb-Douglas utility function is correct, the
among of milk purchased by the household should be log-linear, with
coefficients on income and the price of milk equal to 1 in absolute
value. We might specify the following regression equation:
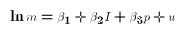
The disturbance term u accounts for different tastes for
milk across households associated with different values of 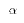 .
Households with the same income and facing the same prices might have
different milk consumptions because of differences in tastes: for
example, one
household might have young children which would push up total milk
consumption.
.
Households with the same income and facing the same prices might have
different milk consumptions because of differences in tastes: for
example, one
household might have young children which would push up total milk
consumption.
Even with tastes differing across households, the Cobb-Douglas model
implies two hypotheses about the MLRM:  = 1 and
= 1 and 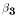 = -1.
These hypotheses might be
interesting to test given data on milk prices, household income, and
household consumption of milk.
= -1.
These hypotheses might be
interesting to test given data on milk prices, household income, and
household consumption of milk.
But notice that this demand function has two variables: income and
milk prices. We could certainly estimate a simple linear regression model
including only one variable or the other (either price or income). But
since both variables can be measured much less would be left to the
residual term if both were included in the analysis. The Multiple LRM is
generalizes the simple LRM to allow two or more variables on the right hand
side of the PRE.
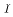 be
household
income. Suppose the household has the utility function
be
household
income. Suppose the household has the utility function
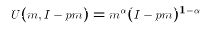
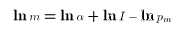
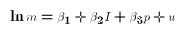
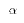 .
Households with the same income and facing the same prices might have
different milk consumptions because of differences in tastes: for
example, one
household might have young children which would push up total milk
consumption.
.
Households with the same income and facing the same prices might have
different milk consumptions because of differences in tastes: for
example, one
household might have young children which would push up total milk
consumption.
 = 1 and
= 1 and 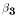 = -1.
These hypotheses might be
interesting to test given data on milk prices, household income, and
household consumption of milk.
= -1.
These hypotheses might be
interesting to test given data on milk prices, household income, and
household consumption of milk.