Linear independence means that no column can be written as a linear
combination of the others. You might recall that this is the
same as saying that X has
full rank. You may be tempted to distribute the
inverse operator through the matrix multiplication:
Now X is simply a column of 1's and
must have full rank. X'X then equals the scalar N (because it equals
1*1+1*1+...+1*1 = N. The matrix X'y simply equals the sum of Y values in the sample.
So the OLS estimate
This is the case studied as the Simple LRM. You should verify that:
In this case we have as many parameters to estimate as we have observations. We
have N equations in N unknowns. As long as X (which is now square N x N and k x k since
N=k)
has an inverse, then OLS will find the estimates that satisfy the equation
Exercise: use these formulas to derive computational properties of
OLS estimates for the MLRM that are analogous to those derived for the simple
LRM.
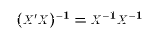
If this is possible, then 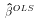 reduces to
reduces to 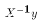 . But note that one
can distribute the inverse operator only if each matrix in the multiplication
has an inverse. X is a k x N, and can only have an inverse if k=N, because only
square matrices have inverses. Therefore, if
. But note that one
can distribute the inverse operator only if each matrix in the multiplication
has an inverse. X is a k x N, and can only have an inverse if k=N, because only
square matrices have inverses. Therefore, if 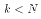 then it is not possible to
simplify (***) any more.
then it is not possible to
simplify (***) any more.OLS estimates in 3 Special Cases of the MLRM
Using the derived formulas for the OLS estimates we get the OLS prediction
and error formulas:
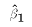 reduces to
reduces to 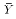 when only
a constant term is included in the regression.
when only
a constant term is included in the regression. 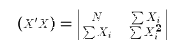
Then you should use the formula for the inverse of a 2x2 matrix to get
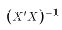 . With some manipulation it is possible to show that (***)
gives back exactly the scalar formulas for
. With some manipulation it is possible to show that (***)
gives back exactly the scalar formulas for 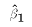 and
and
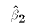 for the case k=2.
for the case k=2.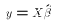 , which is simply
, which is simply 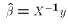 . But we already have seen that
(***) collapses to this expression if X is invertible. The prediction error is
identically 0 for each observation because we can perfectly explain each observation.
If X is not invertible, then we cannot find N different values of
. But we already have seen that
(***) collapses to this expression if X is invertible. The prediction error is
identically 0 for each observation because we can perfectly explain each observation.
If X is not invertible, then we cannot find N different values of 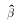 . We
know longer have a system of linearly independent equations because X is no longer
full rank.
. We
know longer have a system of linearly independent equations because X is no longer
full rank.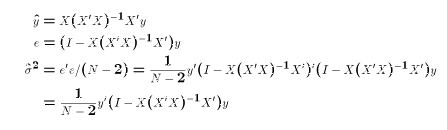
Note that each of these expressions except the last takes the form "some matrix that
involves only X" X the vector y. In other words, each is a linear function of the Y
observation in the sample. The final expression is different since it includes y' and
y. The last step in deriving the matrix expression for 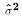 is proved in
class.
is proved in
class.
This document was created using HTX, a (HTML/TeX) interlacing program written by Chris Ferrall.
Document Last revised: 1997/1/5

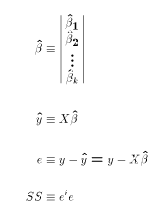
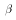 minimize the scalar function SS. In class we derive the
OLS estimator for the MLRM:
minimize the scalar function SS. In class we derive the
OLS estimator for the MLRM:
