Queens University at KingstonHyperEconometricsNotesCFerrall

multiple File 9
[multiple Contents] [Previous File] [Next File]

I. Analysis of Variance

The analysis of variance interpretation of OLS works exactly the same way in the MRLM as the Simple LRM. In particular, OLS estimates decompose the total variation in Y around the sample mean into two components: explained variation and unexplained or residual variation. So TSS = RSS + ESS. The only differences is that RSS, ESS, and TSS must be extended to matrix notation.
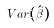
$$\displaylines{ RSS = y'(I- X(X'X)^{-1}X')y\cr M \equiv \hbox{NxN matrix of ones}\cr (I -{1\over N}M)'(I-{1\over N}M) = I - {1\over N}M TSS = y'(I - {1\over N}M)y\cr ESS = y' (X(X'X)^{-1}X' - {1\over N}M)'(X(X'X)^{-1}X' -{1\over N}M) y\cr R^2 \equiv {ESS\over TSS}\cr }$$

J. Violation of LRM Assumptions LRM and OLS Estimates

  1. Violation of A0

    if the data do not contain all the data then one cannot compute all of the OLS estimates, so violation of this assumption is fatal to estimating the full model.

  2. Violation of A1

    there are many reasons to think about how the form of the Population Regression Equation may be wrong. Perhaps one is not sure that the PRE should be linear, log-linear, or some other transformation of the original data. Even worse, perhaps the relation between Y and X can't be linearized at all. That is one way to think about the logit and probit models - as extensions of the OLS model in which the relationship between Y and X is a specific one that cannot fit into the LRM framework.

  3. A2

    If the PRE did not generate the sample information then some other process did. So violation of these assumptions is in many respects equivalent to the violation of A1.

  4. A3

    As mentioned in the original discussion of the assumptions, A3 is really a technical assumption. If E[u] is not zero then one can re-define $\beta_1$ to include the mean of u.

  5. Violation of A4

    Recall that under A0-A4 OLS estimates are unbiased estimates of the LRM parameters. Violating Assumptions A0-A3 leads to either trivial changes (in the case of A0 and A3) or fairly esoteric statistical issues of what model seems to be generating the data. I call this esoteric because it tends to lead one away from the economic content of the LRM, unless one looks for other specifications that come from economic theory. However, most analysis of violations of A1 and A2 are not based on economic theory.

    Violation of A4/A4* is another matter altogether. If cov(u,X) is not 0 (the A4* way of seeing it), or if one cannot think of X as "exogenous" to Y (the A4 way), then one is in trouble. And this trouble has a lot to do with economic theory. A whole chapter on IQ scores is devoted to explaining why A4 is a critical assumption.

  6. Violation of A5-A6

    Traditionally one would go from this point to study ways to "fix" OLS estimates when A5 and A6 do not hold. But it is important that these assumptions only enter at the point of deriving $Var(\hat\beta)$ . This means estimated standard errors and confidence intervals won't be good if A5 and/or A6 is not true. However, this is in many ways a much smaller problem than having either a non-linear model or not even having unbiased estimates. Therefore, our discussion of these assumptions is brief.

  7. Violation of A7

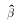    Since OLS estimates are linear in the Y's, violation of the normality assumption is really only a problem in small samples. That's because for values of N larger than 30 the Central Limit Theorem begins to kick in. That is $\hat\beta$ will be asymptotically normally distributed even if u is not normally distributed.

End of Document multiple

[multiple Contents] [Previous File]