HyperMetricsCFerrallHyperMetricsCFerrallThe conclusion drawn from a regression or any other statistical procedure should NEVER be an answer, but rather a better QUESTION. One of the most important episodes concerning the use of regression to give answers rather than questions is the history of studying IQ tests.
The Intelligence Quotient (IQ) was developed by Binet as a way to identify students who are falling behind their peers and could benefit from extra attention. Like many useful tools, it was quickly used incorrectly. Almost from the start scientists (typically white male scientists of European heritage who were themselves misinterpreting and misapplying Darwin's theory of evolution), began trying to see whether IQ tests differed across races and the sexes.
Of course, they were convinced a priori that white males would have the highest scores. The tools of regression and correlation being developed at the time helped make the point. We can trace this story through a series of regressions. While this is not historically accurate because much of the notation, methodology, and rhetoric has changed over the years, this way of telling the story makes the essential points and uses our framework exclusively. (References to other accounts are given at the end of the document).
So it is reasonable to assume that the
But perhaps instead we should make sure that there aren't other important
variables at play that are correlated with the included variables. The
most striking element of the education system in much of the U.S. until
after 1954 was segregation by race. Blacks attended separate schools that
were anything but equal. Teachers in black schools were paid less,
trained less, and worked with poorer supplies. Maybe one year of
education for a white person provided better training that one year of
education for a black person.
In other words, school quality may be omitted in (2) because years of
education captures only quantity and not quality. Consider the population
regression model:
B. The First Wave
One of the biggest coups for "proving" this point came during World War I
when American psychologists convinced the U.S. Army to administer IQ tests
to all recruits and to record control variables such as race. We can
think of the first results as coming from a regression of the form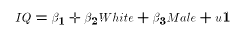
where White is a dummy variable indicating the person is white, and
Male a dummy variable indiciating a man. The error term u1 is the
error associated with the specification (1). It came as no surprise that
the estimates of 
and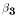 
were positive and significantly
different from 0. This supported the hypothesis that men and white people
have greater intellect than others.
C. The Second Wave
But, of course, ability to perform well on a IQ test depends upon many
things, not simply (and maybe not at all!) the genetic factors White and
Male. Consider the effect of race. In the early 1900s, most American
blacks lived in the south and had access to almost no education. Equation
(1) does not control for this fact, differences in education levels are
captured in the error term u1. If we expand (1) to be of the form
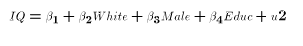
where Educ is the number of years of school attended by the person
before the test was administered. If (1) is estimated the effect of
Educ is included in u1, but is not included in u2. Suppose
Educ does have an effect on IQ even though the researchers
tried to make the test a measure of only inate ability. (At the least the
IQ test had to be given orally if the person couldn't read and reading
is certainly not inate.)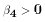 
. How does excluding
this variable affect estimates of
and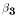
? We know that
the estimate of
from equation (1) would have the property:
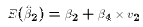
where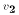 
is the estimated coefficient in the regression:
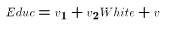
Given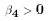 
and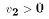 
(whites went to school longer than blacks),
the estimate of
from (1) is biased upwards:
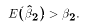
The effect of race is overestimated when education is omitted. Again, the
point isn't just that Educ is related to IQ and is excluded from
equation (1). It is that Educ is related to IQ AND it is correlated with
White (and in the past Male as well). Of course, there were reasonable
white male scientists who saw through this issue at the time, so it was
only the ones who wanted to be convinced that were.
D. The Third Wave
If you were to run equation (2) using data from the 1920s in the U.S., you
would still get a positive and significant coefficient on the White variable
even after controlling for education. Perhaps we should conclude that there
is still a genetic racial difference in IQ after all.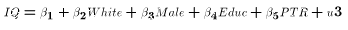 
where PTR stands for pupil-teacher-ratio in the school system the person
attended. We might expect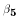 
to be negative - the more pupils per
teacher the less good the education and the lower IQ scores are, all else
constant. And PTR was negatively correlated with White because whites went
to schools with more teachers per student (and better books and better
equipment and ...). If 
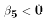and White negatively correlated with
PTR, then the race indicator is picking up both the effect of race and the
indirect effect of school quality. This leads to an overestimate of b2
using equation (2).
Meet the New Bias: Same as the Old Bias
Finally, one could bring the story up to the 1970s or so, by introducing
the fact that IQ tests themselves are a biased measure of intelligence,
because they are based on "white" culture. We could then think that the
true (and politically correct) model looks something like:
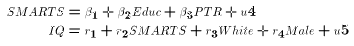
where SMARTS is some unmeasurable index of "intelligence".
IQ is related to smarts, but may also culturally
determined, as indicated by other factors in (4.2).
(4.1) and (4.2) do
not allow a direct link between Smarts and race and sex.
E. Summary
The point of this story IS NOT:
F. References
End of Document iqscores
[iqscores Contents] [Previous File]